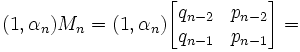The details of today's blog is based on Harold M. Stark's An Introduction to Number Theory.
Lemma 1: if δ(1,√d) = (1,√d)Mn-1Mn+kj, then there exists rk, sk, tk, uk such that:
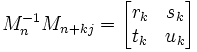
and
(dtk - sk) + (rk - uk)√d = 0.
(1) By assumption, we let:
δ(1,√d) = (1,√d)Mn-1Mn+kj [See here for an example where this assumption is true]
(2) Further, since we know that Mn-1 is a 2 x 2 matrix (see here), we know that the product with Mn+kj is a 2x2 matrix (see here) and we can assume that there exists rk, sk, tk, uk such that:
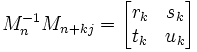
(3) Now, we know that:
δ(1,α) = (δ,δα) [See here for review of matrix math]
(4) From a previous result, we know that:
δ(1,α) = (1,α)Mn-1Mn+j [See here]
(5) Combining #4 and #5 with #2 gives us:
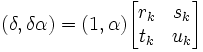
(6) From #6 (see here for review of matrix math), we can conclude that:
(δ, δα) = (rk+tkα, sk+ukα)
(7) This means that:
δ = rk + tkα
δα = sk + ukα
(8) Combining these two equations gives:
(rk + tkα)α = sk + ukα
(9) Which means that:
rkα + tkα2 = sk + ukα
(10) And subtracting the left-side value from both sides give us:
tkα2 + rkα - ukα - sk = 0
which is:
tkα2 + α(rk - uk) - sk = 0
(11) Since we know that α = √d (see here for review of α)
tkα2 + α(rk - uk) - sk = tkd +√d (rk - uk) - sk
(12) So, this gives us finally:
(dtk - sk) + (rk - uk)√d= 0.
QED
Lemma 2: Mn = Mm → n = m.
(1) Assume that Mn = Mm but n ≠ m
(2) Mn =
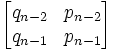
(3) Mm =
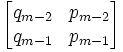
(4) Since Mn = Mm, we have:
qn-2 = qm-2
qn-1 = qm-1
(5) Now q1 is less than q2 and so on (see here for proof). So, m-2, n-2, n-1, m-1 must all be less than 1. (Otherwise, they cannot be equal)
(6) q0 and q-2 = 1 while q-1 = 0.
(7) So, m-2, n-2, n-1, m-1 cannot equal -1. [Since by #6 no other value = 0]
(8) On the other, it is possible for q-2 = q0 = q1 since all could = 1. (See here and here)
(9) So n-2, m-2, n-1, m-1 must equal -2,0, or 1.
(10) So n must = 2 (so that n-1 = 1, n-2 = 0). [Note: n=0 doesn't work since n-1 = -1; n=1 doesn't work since n-2=-1; and n=3 doesn't work since n-1 = 2]
(11) But then m must also = 2 (so that m-1=1, m-2=0) but this goes against our assumption.
(12) So we have a contradiction. There is no way that Mn = Mm without n = m.
QED