In today's blog I continue the proof for the Principle of Quadratic Reciprocity. If you are not familiar with the concepts of quadratic reciprocity, quadratic residues, or the Legendre Symbol start here.
If you would like to start this proof at the beginning, start here.
If you are not familiar with the Legendre Symbol, you should review here.
Today's proof is taken from Gareth A. Jones and J. Mary Jones' Elementary Number Theory.
Definition 1: Reduced Set of Residues mod n
R is a reduced set of residues mod n if it contains each of the congruence classes in Un [See here for a definition of Un]
Examples:
Reduced set of residues mod (8) = { 1, 3, 5, 7 }
(1)(1) ≡ 1 (mod 8)
(3)(3) ≡ 1 (mod 8)
(5)(5) ≡ 1 (mod 8)
(7)(7) ≡ 1 (mod 8)
Lemma 1: if p is an odd prime, φ(p) = p-1
This is clear since all items 1..p-1 are relatively prime to p. [See here for definition of φ(p)]
QED
Lemma 2: There are exactly φ(n); elements in the reduced set of residues mod n.
(1) φ(n) ≤ the number of elements in the reduced set of residues mod n.
(a) φ(n) counts the number of integers a where gcd(a,n)=1.
(b) By Bezout's Identity, there exists u,v au + nv = 1
(c) But then au-1 = -nv which means that au ≡ 1 (mod n)
(d) So each integer a counted by φ(n) is a unit. [See here for definition of modular units]
(2) But, also, the total number of elements in the reduced set of resides ≤ φ(n)
In other words, if gcd(a,n) is greater than 1, then a is not a unit since:
(a) Let us suppose that gcd(a,n)=d which is greater than 1 and n divides ab-1. [n divides ab-1 since we ab ≡ 1 (mod n) ]
(b) By definition of gcd, there exists an integer a' such that a = da'
(c) Since n divides ab-1, there exists b' such that ab-1 = nb'
(d) Now, since d divides ab and d divides nb', it must divide 1 which is impossible.
(e) So we have a contradiction.
(3) So if the reduced set is ≤ φ(n) and φ(n) ≤ the reduced set, it follows that the reduced set = φ(n).
QED
Lemma 3: if R is a reduced set of residues mod (n) and gcd(a,n)=1, then the set aR is also a reduced set of residues mod (n).
(1) Since R is a reduced set, we know that each of its elements are units. [See Definition of Reduced Set above]
(2) Since gcd(a,n)=1 and since r ∈ R → gcd(r,n)=1 [See Lemma 2 above], we know that gcd(ar,n)=1.
(3) So, each of the aR are also units [See the reasoning in Lemma 2 above to see how gcd(ar,n)=1 proves that it is a unit]
(4) Let r,r' be elements of the reduced set R.
(5) ar ≡ ar' (mod n) → r ≡ r' (mod n) [See here for review of modular arithmetic]
(6) Likewise r not ≡ r' → ar is not congruent to ar' since:
(a) Assume that r not ≡ r' (mod n) but ar ≡ ar' (mod n)
(b) From the reasoning in #5, ar ≡ ar' (mod n) tells us that r ≡ r' which is a contradiction so we reject our assumption (a).
(7) If all the elements aR are units and r not ≡ r' → ar not ≡ ar' tells us that there is a one-to-one correspondence between R and aR.
(8) And this tells us that aR is also a reduced set of residues modulo n.
QED
Theorem: Euler's Theorem
If gcd(a,n)=1, then aφ(n) ≡ 1 (mod n)
(1) We know that φ(n) is between 1 and n-1. [See here for definition of φ(n)]
(2) We can set R = the set { 1, 2, ... φ(n) }
(3) Since gcd(a,n)=1, we know that (see Lemma 3 above):
aR has a one-to-one correspondence with R in terms of congruences.
(4) This gives us that:
a*2a*..*φ(n)a ≡ 1*2*...*φ(n) (mod n)
(5) But then we get:
aφ(n)*(1*2*...*φ(n)) ≡ 1*2*...*φ(n) (mod n)
(6) Dividing both sides by 1*2*...*φ(n) gives us (see here for a review of modular arithmetic)
aφ(n) ≡ 1 (mod n)
QED
Saturday, February 11, 2006
Wednesday, February 08, 2006
Units for Modular Arithmetic
In today's blog I continue the proof for the Principle of Quadratic Reciprocity. If you are not familiar with the concepts of quadratic reciprocity, quadratic residues, or the Legendre Symbol start here.
If you would like to start this proof at the beginning, start here.
If you are not familiar with the Legendre Symbol, you should review here.
Today's proof is taken from Gareth A. Jones and J. Mary Jones' Elementary Number Theory.
Definition 1. Up: Set of units modulo p.
x ∈ Up if and only if there exists y such that xy ≡ 1 (mod p).
As should be clear, in all the cases above, both x,y ∈ Up
Definition 2. Primitive Root Modulo p
x is a primitive root for a set S if for any y ∈ S, y ≡ xi (mod p) where i ≥ 1.
Example: 2 is a primitive root for U3
By Definition 1, U3 = { 1, 2 } since (1)(1) ≡ 1 (mod p) and (2)(2) ≡ 1 (mod p).
But then:
1 ≡ 22 (mod p)
2 ≡ 21 (mod p)
Definition 3: Cyclic set
A set is cyclic if there exists at least one element that is a primitive root.
Example: U3 is cyclic since it has a primitive root of 2.
Definition 4: Order of an element of Up
The order of x ∈ Up is the least element i such that xi ≡ 1 (mod p).
Example:
1 has an order of 1 in U3 [See Definition 2 example for details]
2 has an order of 2 in U3
Definition 5: Euler's Function: φ(n)
φ(n) = the number of elements a such that gcd(a,n)=1
Example:
φ(2) = 1 since gcd(1,2)=1
φ(3) = 2 since gcd(1,3)=1 and gcd(2,3)=1
φ(4) = 2 since gcd(1,4)=1 and gcd(3,4)=1
etc.
Lemma 1: If p is an odd prime, the order of each element of Up divides p-1.
(1) Let a be an element of Up
(2) ap-1 ≡ 1 (mod p) [By Fermat's Little Theorem, see here]
(3) Now we can assume that the order is less than p-1.
If order(a) = p-1, then we are done since p-1 divides p-1.
It cannot be greater than p-1 since the order is the smallest number greater than 0 and p-1 is greater than 0.
(4) Let d be the order for this element a.
(5) Assume that d does not divide p-1.
(6) Using the Division Algorithm (see here), we know that there exists q,r such that:
p-1 = qd + r
r is greater than 0 (by step #5)
r is less than d (by the Division Algorithm)
(7) So, ap-1 ≡ aqd + r ≡ aqd * ar [See here if you need a review of exponents]
(8) Now, since aqd ≡ (ad)q, we have:
aqd ≡ 1 (mod p)
(9) Combining (#8) with (#7) gives us:
ap-1 ≡ (1)*ar ≡ ar
(10) But ap-1 ≡ 1 (mod p) so ar ≡ 1 (mod p)
(11) And this is a contradiction since r is less than d but d is the lowest value where ad ≡ 1 (mod p).
(12) So we reject our assumption at #5.
QED
Lemma 2: if a ≠ 0 and a is a positive integer less than p odd prime p, then a ∈ Up.
(1) gcd(a,p)=1
(2) There exists u,v such that au + pv = 1. [Bezout's Identity, see here]
(3) Then, au - 1 = -pv
(4) Then au ≡ 1 (mod p) [See here for review of modular arithmetic]
(5) Then a is a unit mod p [By definition of unit mod p above]
QED
Corollary 2.1 There are p-1 elements in Up
This follows directly from Lemma 2 above.
Lemma 3: if gcd(a,n)= n/d and a = (n/d)a', then gcd(a',d) = 1
(1) Assume gcd(a',d) = g which is greater than 1.
(2) g divides a' and g divides d
(3) There exists u,v such that gu=a', gv=d
(4) (ng)/d is greater than (n)/d since g is greater than 1.
(5) a = (n/d)*a' = (n/d)*gu = (ng/d)*u
(6) n = (n/d)*d = (n/d)*gv = (ng/d)*v
(7) But then (ng)/d divides a and (ng)/d divides n and (ng/a) is greater than (n/d)
(8) But (n/d) is gcd(a,n) so we have a contradiction.
(9) Therefore, we reject our assumption in #1.
QED
Lemma 4: The sum of φ(n) such that (d divides n) = n.
(1) Let S be a set = { 1, 2, 3, ..., n }
(2) Let Sd = the set of elements a in S where gcd(a,n) = n/d.
For example, let's consider n=8.
S2 = elements a where gcd(a,8) = 8/2 = 4 = { 4 }
S4 = elements a where gcd(a,8) = 8/4 = 2 = { 2 }
S8 = elements a where gcd(a,8) = 8/8 = 1 = { 1, 3, 5, 7}
Another example, let's consider n = 12
S2 = elements a where gcd(a,12) = 12/2 = 6 = { 6 }
S3 = elements a where gcd(a,12) = 12/3 = 4 = {4, 8}
S4 = elements a where gcd(a,12) = 12/4 = 3 = {3, 9}
S12 = elements a where gcd(a,12) = 12/12 = 1 = { 1, 5, 11}
(3) We note that the total # of all Sd = n since:
(a) Let b = gcd(a,n)
(b) By definition b divides n [otherwise, n ≠ gcd(a,n)]
(c) There exists c such that n = bc and we see that b = n/c
(d) So we see that b ∈ Sc
(e) We also note that each element is only in 1 Sd since d = n/gcd(a,n)
(4) Let a' = (ad)/n for any integer a in Sd
(5) a' is an integer since:
(a) d=n/gcd(a,n)
(b) a' = (ad)/n = (a)[n/gcd(a,n)]/n = (an)/(gcd(a,n)n) = a/gcd(a,n)
(c) We know that gcd(a,n) divides a by definition of gcd (see here if more info needed)
(6) gcd(a',d) = 1 since a = (n/d)*a' [From Lemma 3 above]
(7) Now, we see for each Sd there is a one-to-one correspondence between this element and the value a' where:
(a) a' is between 1 and d [since a' = ad/n and a is between 1 and n]
(b) gcd(a',d)=1 [from #6]
(c) the total number of elements a' = φ(d) [By definition of φ(d) ]
(8) So, #7 gives us that the total number of elements for any Sd = φ(d)
(9) By Step #3, we can put this all together to give us: the sum of φ(d) for d that divide n = n.
QED
Lemma 5: if a is an element of Up and order(a)=d, then a1, a2, ..., ad are distinct modulo p.
(1) Let k = order of a.
(2) We can assume that k is greater than 2.
If k=1, then we are done since there is only 1 element a1
If k=2, then we are done since we have 2 distinct elements a1 and a2.
(3) Let's assume that that the set of elements is not distinct.
(4) Then, there exists some u,v such that:
1 ≤ u is less than k
1 ≤ v is less than k
u ≠ v
au ≡ av (mod p)
We can assume that u,v are less than k since ak ≡ 1 (mod p) and order(a)=k implies that no other ai = 1 (by definition of order).
(5) Let's assume that u is less than v
Since u ≠ v, we can assume label the smaller one u and the larger one v.
(6) We know that there exists t such that t = k - v and t ≥ 1 so that k = t + v
(7) at*av ≡ ak ≡ 1 (mod p)
(8) But since au ≡ av (mod p), then we have:
at*au ≡ at+u ≡ 1 (mod p)
(9) But u + t is less than k since u is less than v and since k = t + v.
(10) And this is impossible since k is the order. So we have a contradiction and we reject our asusmption in #3.
QED
Lemma 6: x - h divides xi - hi
(1) Case i = 1, 2, 3
x - h divides x1 - h1
x2 - h2 = (x + h)(x - h)
x3 - h3 = (x - h)(x2 + h2 + hx)
(2) Assume that x-h divides up to some value xn - hn such that x ≥ 3.
(3) hxn - hnx = hx(xn-1 - hn-1)
(4) Now x-h divides xn-1 - an-1 by our assumption in #2.
(5) So x-h divides hxn - hnx
(6) Now xn+1 - hn+1 = (xn + hn)(x - h) + hxn - hnx.
(7) Since x-h divides hxn - hnx, using (#6), we find that it must also divide xn+1 - hn+1.
(8) So, we apply the principle of induction and we are done.
QED
Lemma 7: Lagrange's Theorem
Let anxn + an-1xn-1 + ... + a1x + a0 ≡ 0 (mod p) where ai is not divisible by p for some i, then there are at most n roots that satisfy this equation.
(1) Case n = 0
If n=0, then there is only a0 which is not divisible by p. Therefore, there are no solutions.
(2) Now assume that it is true up to n-1 so for each equation an-1xn-1 + ... + a1x1 + a0 ≡ 0 (mod p), there are at most n-1 solutions.
(3) Let f(x) = anxn + ... + a1x + a0
(4) We can assume that there is at least one solution h such that f(h) ≡ 0 (mod p)
If there was no solution, then we have shown that the total number of solutions is ≤ n.
(5) So f(x) - f(h) =
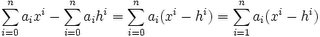
NOTE: We switch i to 1 since x0 - h0 = 0.
(6) From Lemma 6, we know that x - h divides xi - hi
(7) So for each i in (#5), we have:
xi - hi = (x - h)(xi-1 + hxi-2 + ... + hi-2x + hi-1)
(8) Let g(x) = the sum of all equations created by #7. This then gives us:
f(x) - f(h) = (x-a)g(x)
(9) By our assumption in #2, we can assume that g(x) has at most n-1 solutions whereby g(x) ≡ 0 (mod p) since:
(a) g(x) has integer coefficients (from Lemma 6)
(b) p cannot divide all the coefficients of g(x) since;
If it did, it would divide g(x) and it would divide f(h), and this would mean that it would divide f(x).
But it cannot divide f(x) since by assumption it does not divide all the ai.
Therefore, p cannot divide all the coefficients.
(10) For each solution of f(x), we know that it must divide f(x) - f(h) and therefore, it must divide (x-h)g(x).
(11) This means that for each solution of f(x), p either divides (x-h) or p divides g(x).
(12) Now, there is only one solution that solves for x-h.
(13) And, there are at most n-1 solutions that solve for g(x).
(14) So, there are a total of n solutions that solve for (x-h)g(x).
QED
Lemma 8: if a is an element of Up with order(a) = d, then there exists b,i such that a ≡ bi (mod p) and 1 ≤ i ≤ d and gcd(i,d)=1.
(1) By Lemma 5 above, the set of elements in Up with order=d consist of b1, b2, ..., bd.
(2) But we note that all elements of order=d solve the equation xd - 1 ≡ 0 (mod p) [By the definition of Order]
(3) From Lemma 7 above, we know that there are at most d solutions to xd - 1 ≡ 0 (mod p) so we know that the items lists in #1 are the complete set.
(4) So, there must exist a value i such that a ≡ bi (mod p).
(5) Let j = gcd(i,d)
(6) ad/j ≡ b(id/j) ≡ (bd)i/j ≡ 1i/j ≡ 1 (mod p)
(7) But if j is greater than 1, then d/j is less than d which is impossible since d is the order [see definition of order above]
(8) So, j = 1.
QED
Lemma 9: If w(d) is the number of elements in Up that have order = d, then w(d) ≤ φ(d)
(1) We can assume that w(d) ≥ 1.
If there are no elements with order d, then we have w(d)=0 which is less than φ(d).
(2) From (#1), for each order, we know that there exists an element a such that order(a)=d.
(3) We also know each value a1, a2, ... ad are distinct mod p. [See Lemma 5]
(4) Each value ai in (#3) solves the polynomial ad ≡ 1 (mod p) since:
(ai)d ≡ adi ≡ (ad)i ≡ 1 (mod p) [By the definition of order, see above]
(5) Now, ad - 1 has at most d roots. [See Lemma 7]
(6) So, the elements in #3 are the complete set of roots.
(7) Now, if we take the set of all elements a that have order(a)=d, there exists some b,i such that a ≡ bi (mod p), then 1 ≤ i ≤ d and gcd(i,d)=1. [See Lemma 8]
(8) From (#7), we know that there is a one-to-one correspondence between the number of elements that have order(a) = d and the value bi where i is between 1 and d and gcd(i,d)=1.
(9) So that, from (#8), we know that the total number of elements a that have order(a)=d is none other than φ(d).
QED
Lemma 10: If p is a prime, then Up has φ(d) elements of order d for each d that divides p-1.
(1) Let w(d) = the number of elements in Up that have the order = d.
(2) The order of each element divides p-1. [See Lemma 1]
(3) The total of all w(d) such that (d divides p-1) = p-1.
There are p-1 elements that make up Up. [See Corollary 2.1 above]
Each element has a unique order. [See definition of Order above]
Each order must divide p-1 [by Lemma 1]
So, all elements have an order that divides p-1, so the total w(d) = p-1.
(4) The sum of all φ(d) such that (d divides p-1) = p-1. [See Lemma 4]
(5) The total for each d that divides n of (φ(d) - w(d)) = p-1 - (p-1) = 0.
(6) Now w(d) ≤ φ(d). [See Lemma 9]
(7) So w(d) = φ(d) [By combining #5 and #6]
QED
Theorem 1: If p is an odd prime, then Up is cyclic with order p-1.
(1) There exists an integer d such that d = p-1.
(2) There are φ(p-1) elements of order p-1 in Up [See Lemma 10]
(3) Since φ(p-1) ≥ 1 (see definition of φ(x) above), the group contains at least one element of order=p-1. Let's call this element a. [See Lemma 10]
(4) But we also know that a1, a2, ... ap-1 are distinct. [By Lemma 5 above]
(5) So, by definition, a is a primitive root for Up and Up is cyclic [See Definition 3 and Definition 4 above]
QED
If you would like to start this proof at the beginning, start here.
If you are not familiar with the Legendre Symbol, you should review here.
Today's proof is taken from Gareth A. Jones and J. Mary Jones' Elementary Number Theory.
Definition 1. Up: Set of units modulo p.
x ∈ Up if and only if there exists y such that xy ≡ 1 (mod p).
As should be clear, in all the cases above, both x,y ∈ Up
Definition 2. Primitive Root Modulo p
x is a primitive root for a set S if for any y ∈ S, y ≡ xi (mod p) where i ≥ 1.
Example: 2 is a primitive root for U3
By Definition 1, U3 = { 1, 2 } since (1)(1) ≡ 1 (mod p) and (2)(2) ≡ 1 (mod p).
But then:
1 ≡ 22 (mod p)
2 ≡ 21 (mod p)
Definition 3: Cyclic set
A set is cyclic if there exists at least one element that is a primitive root.
Example: U3 is cyclic since it has a primitive root of 2.
Definition 4: Order of an element of Up
The order of x ∈ Up is the least element i such that xi ≡ 1 (mod p).
Example:
1 has an order of 1 in U3 [See Definition 2 example for details]
2 has an order of 2 in U3
Definition 5: Euler's Function: φ(n)
φ(n) = the number of elements a such that gcd(a,n)=1
Example:
φ(2) = 1 since gcd(1,2)=1
φ(3) = 2 since gcd(1,3)=1 and gcd(2,3)=1
φ(4) = 2 since gcd(1,4)=1 and gcd(3,4)=1
etc.
Lemma 1: If p is an odd prime, the order of each element of Up divides p-1.
(1) Let a be an element of Up
(2) ap-1 ≡ 1 (mod p) [By Fermat's Little Theorem, see here]
(3) Now we can assume that the order is less than p-1.
If order(a) = p-1, then we are done since p-1 divides p-1.
It cannot be greater than p-1 since the order is the smallest number greater than 0 and p-1 is greater than 0.
(4) Let d be the order for this element a.
(5) Assume that d does not divide p-1.
(6) Using the Division Algorithm (see here), we know that there exists q,r such that:
p-1 = qd + r
r is greater than 0 (by step #5)
r is less than d (by the Division Algorithm)
(7) So, ap-1 ≡ aqd + r ≡ aqd * ar [See here if you need a review of exponents]
(8) Now, since aqd ≡ (ad)q, we have:
aqd ≡ 1 (mod p)
(9) Combining (#8) with (#7) gives us:
ap-1 ≡ (1)*ar ≡ ar
(10) But ap-1 ≡ 1 (mod p) so ar ≡ 1 (mod p)
(11) And this is a contradiction since r is less than d but d is the lowest value where ad ≡ 1 (mod p).
(12) So we reject our assumption at #5.
QED
Lemma 2: if a ≠ 0 and a is a positive integer less than p odd prime p, then a ∈ Up.
(1) gcd(a,p)=1
(2) There exists u,v such that au + pv = 1. [Bezout's Identity, see here]
(3) Then, au - 1 = -pv
(4) Then au ≡ 1 (mod p) [See here for review of modular arithmetic]
(5) Then a is a unit mod p [By definition of unit mod p above]
QED
Corollary 2.1 There are p-1 elements in Up
This follows directly from Lemma 2 above.
Lemma 3: if gcd(a,n)= n/d and a = (n/d)a', then gcd(a',d) = 1
(1) Assume gcd(a',d) = g which is greater than 1.
(2) g divides a' and g divides d
(3) There exists u,v such that gu=a', gv=d
(4) (ng)/d is greater than (n)/d since g is greater than 1.
(5) a = (n/d)*a' = (n/d)*gu = (ng/d)*u
(6) n = (n/d)*d = (n/d)*gv = (ng/d)*v
(7) But then (ng)/d divides a and (ng)/d divides n and (ng/a) is greater than (n/d)
(8) But (n/d) is gcd(a,n) so we have a contradiction.
(9) Therefore, we reject our assumption in #1.
QED
Lemma 4: The sum of φ(n) such that (d divides n) = n.
(1) Let S be a set = { 1, 2, 3, ..., n }
(2) Let Sd = the set of elements a in S where gcd(a,n) = n/d.
For example, let's consider n=8.
S2 = elements a where gcd(a,8) = 8/2 = 4 = { 4 }
S4 = elements a where gcd(a,8) = 8/4 = 2 = { 2 }
S8 = elements a where gcd(a,8) = 8/8 = 1 = { 1, 3, 5, 7}
Another example, let's consider n = 12
S2 = elements a where gcd(a,12) = 12/2 = 6 = { 6 }
S3 = elements a where gcd(a,12) = 12/3 = 4 = {4, 8}
S4 = elements a where gcd(a,12) = 12/4 = 3 = {3, 9}
S12 = elements a where gcd(a,12) = 12/12 = 1 = { 1, 5, 11}
(3) We note that the total # of all Sd = n since:
(a) Let b = gcd(a,n)
(b) By definition b divides n [otherwise, n ≠ gcd(a,n)]
(c) There exists c such that n = bc and we see that b = n/c
(d) So we see that b ∈ Sc
(e) We also note that each element is only in 1 Sd since d = n/gcd(a,n)
(4) Let a' = (ad)/n for any integer a in Sd
(5) a' is an integer since:
(a) d=n/gcd(a,n)
(b) a' = (ad)/n = (a)[n/gcd(a,n)]/n = (an)/(gcd(a,n)n) = a/gcd(a,n)
(c) We know that gcd(a,n) divides a by definition of gcd (see here if more info needed)
(6) gcd(a',d) = 1 since a = (n/d)*a' [From Lemma 3 above]
(7) Now, we see for each Sd there is a one-to-one correspondence between this element and the value a' where:
(a) a' is between 1 and d [since a' = ad/n and a is between 1 and n]
(b) gcd(a',d)=1 [from #6]
(c) the total number of elements a' = φ(d) [By definition of φ(d) ]
(8) So, #7 gives us that the total number of elements for any Sd = φ(d)
(9) By Step #3, we can put this all together to give us: the sum of φ(d) for d that divide n = n.
QED
Lemma 5: if a is an element of Up and order(a)=d, then a1, a2, ..., ad are distinct modulo p.
(1) Let k = order of a.
(2) We can assume that k is greater than 2.
If k=1, then we are done since there is only 1 element a1
If k=2, then we are done since we have 2 distinct elements a1 and a2.
(3) Let's assume that that the set of elements is not distinct.
(4) Then, there exists some u,v such that:
1 ≤ u is less than k
1 ≤ v is less than k
u ≠ v
au ≡ av (mod p)
We can assume that u,v are less than k since ak ≡ 1 (mod p) and order(a)=k implies that no other ai = 1 (by definition of order).
(5) Let's assume that u is less than v
Since u ≠ v, we can assume label the smaller one u and the larger one v.
(6) We know that there exists t such that t = k - v and t ≥ 1 so that k = t + v
(7) at*av ≡ ak ≡ 1 (mod p)
(8) But since au ≡ av (mod p), then we have:
at*au ≡ at+u ≡ 1 (mod p)
(9) But u + t is less than k since u is less than v and since k = t + v.
(10) And this is impossible since k is the order. So we have a contradiction and we reject our asusmption in #3.
QED
Lemma 6: x - h divides xi - hi
(1) Case i = 1, 2, 3
x - h divides x1 - h1
x2 - h2 = (x + h)(x - h)
x3 - h3 = (x - h)(x2 + h2 + hx)
(2) Assume that x-h divides up to some value xn - hn such that x ≥ 3.
(3) hxn - hnx = hx(xn-1 - hn-1)
(4) Now x-h divides xn-1 - an-1 by our assumption in #2.
(5) So x-h divides hxn - hnx
(6) Now xn+1 - hn+1 = (xn + hn)(x - h) + hxn - hnx.
(7) Since x-h divides hxn - hnx, using (#6), we find that it must also divide xn+1 - hn+1.
(8) So, we apply the principle of induction and we are done.
QED
Lemma 7: Lagrange's Theorem
Let anxn + an-1xn-1 + ... + a1x + a0 ≡ 0 (mod p) where ai is not divisible by p for some i, then there are at most n roots that satisfy this equation.
(1) Case n = 0
If n=0, then there is only a0 which is not divisible by p. Therefore, there are no solutions.
(2) Now assume that it is true up to n-1 so for each equation an-1xn-1 + ... + a1x1 + a0 ≡ 0 (mod p), there are at most n-1 solutions.
(3) Let f(x) = anxn + ... + a1x + a0
(4) We can assume that there is at least one solution h such that f(h) ≡ 0 (mod p)
If there was no solution, then we have shown that the total number of solutions is ≤ n.
(5) So f(x) - f(h) =
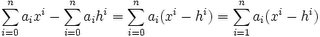
NOTE: We switch i to 1 since x0 - h0 = 0.
(6) From Lemma 6, we know that x - h divides xi - hi
(7) So for each i in (#5), we have:
xi - hi = (x - h)(xi-1 + hxi-2 + ... + hi-2x + hi-1)
(8) Let g(x) = the sum of all equations created by #7. This then gives us:
f(x) - f(h) = (x-a)g(x)
(9) By our assumption in #2, we can assume that g(x) has at most n-1 solutions whereby g(x) ≡ 0 (mod p) since:
(a) g(x) has integer coefficients (from Lemma 6)
(b) p cannot divide all the coefficients of g(x) since;
If it did, it would divide g(x) and it would divide f(h), and this would mean that it would divide f(x).
But it cannot divide f(x) since by assumption it does not divide all the ai.
Therefore, p cannot divide all the coefficients.
(10) For each solution of f(x), we know that it must divide f(x) - f(h) and therefore, it must divide (x-h)g(x).
(11) This means that for each solution of f(x), p either divides (x-h) or p divides g(x).
(12) Now, there is only one solution that solves for x-h.
(13) And, there are at most n-1 solutions that solve for g(x).
(14) So, there are a total of n solutions that solve for (x-h)g(x).
QED
Lemma 8: if a is an element of Up with order(a) = d, then there exists b,i such that a ≡ bi (mod p) and 1 ≤ i ≤ d and gcd(i,d)=1.
(1) By Lemma 5 above, the set of elements in Up with order=d consist of b1, b2, ..., bd.
(2) But we note that all elements of order=d solve the equation xd - 1 ≡ 0 (mod p) [By the definition of Order]
(3) From Lemma 7 above, we know that there are at most d solutions to xd - 1 ≡ 0 (mod p) so we know that the items lists in #1 are the complete set.
(4) So, there must exist a value i such that a ≡ bi (mod p).
(5) Let j = gcd(i,d)
(6) ad/j ≡ b(id/j) ≡ (bd)i/j ≡ 1i/j ≡ 1 (mod p)
(7) But if j is greater than 1, then d/j is less than d which is impossible since d is the order [see definition of order above]
(8) So, j = 1.
QED
Lemma 9: If w(d) is the number of elements in Up that have order = d, then w(d) ≤ φ(d)
(1) We can assume that w(d) ≥ 1.
If there are no elements with order d, then we have w(d)=0 which is less than φ(d).
(2) From (#1), for each order, we know that there exists an element a such that order(a)=d.
(3) We also know each value a1, a2, ... ad are distinct mod p. [See Lemma 5]
(4) Each value ai in (#3) solves the polynomial ad ≡ 1 (mod p) since:
(ai)d ≡ adi ≡ (ad)i ≡ 1 (mod p) [By the definition of order, see above]
(5) Now, ad - 1 has at most d roots. [See Lemma 7]
(6) So, the elements in #3 are the complete set of roots.
(7) Now, if we take the set of all elements a that have order(a)=d, there exists some b,i such that a ≡ bi (mod p), then 1 ≤ i ≤ d and gcd(i,d)=1. [See Lemma 8]
(8) From (#7), we know that there is a one-to-one correspondence between the number of elements that have order(a) = d and the value bi where i is between 1 and d and gcd(i,d)=1.
(9) So that, from (#8), we know that the total number of elements a that have order(a)=d is none other than φ(d).
QED
Lemma 10: If p is a prime, then Up has φ(d) elements of order d for each d that divides p-1.
(1) Let w(d) = the number of elements in Up that have the order = d.
(2) The order of each element divides p-1. [See Lemma 1]
(3) The total of all w(d) such that (d divides p-1) = p-1.
There are p-1 elements that make up Up. [See Corollary 2.1 above]
Each element has a unique order. [See definition of Order above]
Each order must divide p-1 [by Lemma 1]
So, all elements have an order that divides p-1, so the total w(d) = p-1.
(4) The sum of all φ(d) such that (d divides p-1) = p-1. [See Lemma 4]
(5) The total for each d that divides n of (φ(d) - w(d)) = p-1 - (p-1) = 0.
(6) Now w(d) ≤ φ(d). [See Lemma 9]
(7) So w(d) = φ(d) [By combining #5 and #6]
QED
Theorem 1: If p is an odd prime, then Up is cyclic with order p-1.
(1) There exists an integer d such that d = p-1.
(2) There are φ(p-1) elements of order p-1 in Up [See Lemma 10]
(3) Since φ(p-1) ≥ 1 (see definition of φ(x) above), the group contains at least one element of order=p-1. Let's call this element a. [See Lemma 10]
(4) But we also know that a1, a2, ... ap-1 are distinct. [By Lemma 5 above]
(5) So, by definition, a is a primitive root for Up and Up is cyclic [See Definition 3 and Definition 4 above]
QED
Subscribe to:
Posts (Atom)
