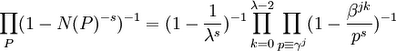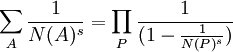Lodovico Ferrari was born on February 2, 1522. His father died when he was very young so he lived with his uncle Vincent Ferrari. The mathematician Gerolamo Cardano was looking for a servant. Vincent's son Luke took the job but decided he didn't like it and left. Cardano then brought the matter up with Vincent. Vincent sent Lodovico to Cardarno in Luke's place.
Lodovico Ferrari was born on February 2, 1522. His father died when he was very young so he lived with his uncle Vincent Ferrari. The mathematician Gerolamo Cardano was looking for a servant. Vincent's son Luke took the job but decided he didn't like it and left. Cardano then brought the matter up with Vincent. Vincent sent Lodovico to Cardarno in Luke's place.On November 30, 1536, fourteen-year old Ferrari became Cardano's servant. Over time, Cardano was very impressed by Ferrari's intelligence and soon began to teach him mathematics. Ferrari began to collaborate with Cardano on his manuscripts and by the time that Ferrari was 18, he began to lecture on mathematics.
In 1540, Ferrari came up with the general solution for the quartic equation. Cardano would later publish this method in his famous book Ars Magna. In 1541, when Cardano resigned his post in mathematics in Milan, Ferrari, then 20, was able to succeed him.
Cardano had earlier solved the general cubic equation which extended a method he had learned from Nicolo Tartaglia. Cardano had promised Tartaglia that he would not publish the method until after Tartaglia published. It was this agreement that held up the publishing of Ars Magna. Cardano was very anxious to publish the work and when he found that Tartaglia's method was based on the method of Scipione del Ferro, he decided in 1545 to publish the work despite his promise to Tartaglia.
Ferrari supported Cardano in the resulting controversy and challenged Tartaglia to a public debate. Ferrari was not yet a well known mathematician so Tartaglia refused to debate him and insisted on challenging Cardano. Nothing happened for three years. Then, in 1548, Tartaglia was offered an important position in mathematics on the condition that he publicly debated Ferrari. By this time, the controversy between the two had become very public and there was a strong popular interest in this mathematical challenge.
The open debate occurred on August 10, 1548 in Milan. It occurred in front of a large crowd. By this time, Ferrari had mastered both the cubic and quartic equations. In the course of the discussion, it was clear that Ferrari was the master of the two and before the contest ended, Tartaglia decided to withdraw. In this way, Ferrari's reputation was greatly established as one of Italy's top mathematicians.
From this point on, Ferrari accepted a series of well paid positions and in 1565, he moved to Bologna where he stayed with his recently widowed half-sister and worked as a professor to the University of Bologna. Within one year, he died very suddenly. It was rumored that he had been poisoned by his half sister who sought to inherit his great wealth. Indeed, after his death, she received all of his estate. Then, she remarried and her husband absconded with all her money.
References
- "Lodovico Ferrari", MacTutor Biography
- "Tartaglia-Cardano Dispute", MacTutor Biography