Niels Abel submitted his impossibility proof for the quintic equation in 1824. Because of lack of funds, he was forced to condense his proof to only 6 pages. This greatly reduced the clarity of the proof. Later, in 1826, Abel published a longer version of his proof that provided additional details. Tragically, in 1829, he grew very sick and died. The great work of Evariste Galois would not come to light until the 1840's.
Even in 1833, Abel's proof was not yet fully accepted by all major mathematical bodies. On that year, George Peacock wrote a report for the British Association for the Advancement of Science where he concluded that "some parts of it are obscure, and not perfectly conclusive."
For the English world, any doubts about Abel's proof would go away with the important work by Sir William Rowan Hamilton. On May 22, 1837, Hamilton presented a paper to the Royal Irish Academy which would settle the issue.
References
Saturday, October 04, 2008
Thursday, October 02, 2008
Sir William Rowan Hamilton
 William Rowan Hamilton was born on August 4, 1805 in Dublin, Ireland. He was the fourth of nine children. Young William showed tremendous intellectual ability very early. By age 5, he had already learned Latin, Greek, and Hebrew.
William Rowan Hamilton was born on August 4, 1805 in Dublin, Ireland. He was the fourth of nine children. Young William showed tremendous intellectual ability very early. By age 5, he had already learned Latin, Greek, and Hebrew.When William was 12, he heard about an American Zerah Colburn who could do impressive calculations all in his head. Hamilton entered a mathematical competition where Zerah had also entered. His loss to Colburn drove him to study mathematics.
At 13, he began to study on his own a classic text on algebra. At 15, he started reading the works of Sir Isaac Newton and Pierre-Simon Laplace. Then, when 18, he started to attract mathematical attention when he found an error in one of Laplace's calculations.
In 1823, he began attending Trinity College. His first year he received an honor (an "optime") in the Classics that is bestowed on students only once every 20 years. Two years later, he received an "optime" in physiccs. For his senior thesis, he wrote an essay where he introducted a function that characterized optics. His outstanding performance at Trinity so astounded the faculty, that the age of 22, before he graduated, he was offered a professorship in astronomy at the college. His title was now Royal Astronomer of Ireland.
Before starting his new position, Hamilton decided to travel to England and Scotland. As part of this trip, he met the poet William Wordsworth. They quickly became friends. While the Royal Astronomer, Hamilton chose to focus on mathematics. He expanded on his senior thesis on a characteristic function in optics. Hamilton showed that the optical properties of a system could be derived from this characteristic function and its partial derivatives.
In 1832, Hamilton built on the theories of Augustin Fresnel and Thomas Young to make predictions about "internal" and "external" conical refraction of light through a crystal. These predictions created quite a stir when they were verified by Humphrey Lloyd through experiment. This was seen as a real triumph of mathematical science.
Between 1834 and 1835, Hamilton published two very important papers on dynamics. Hamilton had found that like optics, dynamics could also be described by a characteristic function. Hamilton introduced what is today called the "Hamiltonian" which is a mathematical form that characterizes the motion of a conservative dynamic system.
It was well known since the time of Carl Friedrich Gauss that the set of complex numbers could be mapped to a 2D coordinate system. Hamilton believed that it should be possible to find a number system that corresponded to a 3D coordinate system. In working through this problem in 1843, Hamilton came up with the concept of "quaternions." This he would consider his greatest achievement. Quaternions was one of the first non-commutative algebras. It is a four-dimensional complex number. In defining quaternion, Hamilton introduced the ideas of scalars and vectors.
When James Clerk Maxwell published his groundbreaking Treatise on Electricity and Magnetism that established the scientific relationship between electricity and magnetism, he used the mathematics of quaternions to state his fundamental equations.
Maxwell's theory of optics initially did not a significant impact on the state of the art. Later, towards the latter part of the nineteenth century, there was a resurgence in their influence and today are used in the design of optical instruments.
Maxwel's theory of dynamics from the beginning was extremely influential in the development of physics. The underyling model was greatly expanded by Carl Jacobi and Hamilton's theory of dynamics played a very influential role in the development of quantum mechanics.
Quaternions was later superceded by the development of modern vector algebra which was developed by Josiah Willard Gibbs and Oliver Heaviside. They created vector algebra as part of an effort to simplify quaternions and to make the subject more intuitive.
Hamilton married in 1833 and had three children, two boys and one girl. He was knighted in 1835. In 1837, he was elected president of the Royal Irish Academy. He held this position until 1846.
Towards the end of his life, Hamilton focused completely on quaternions and continued to extend the length of his treatise on it. He overspent the Trinity funds that were available for this work and his family began to experience financial difficulties. It was during these difficult times that Hamilton grew very sick. He died on September 2, 1865 at the age of 60.
References
- David R. Wilkins, "William Rowan Hamilton: mathematical genius", PhysicsWorld.Com, August 3, 2005
- "Sir William Rowan Hamilton", MacTutor
- "William Rowan Hamilton", Wikipedia
Wednesday, October 01, 2008
Abel's Impossibility Proof
Today's proof is taken from Peter Pesic's translation of Niels Abel's original 1824 proof. A special thanks to Peter for helping me by e-mail! :-)
Abel printed a limited set copies of his proof in hopes of using it as a "calling card" when he visited the great mathematicians of his day. Because he was short on funds, Abel was forced to keep the proof as short and concise as possible. He had hoped to secure recognition and financial sponsorship from his trip. When he ran out of money, he returned to his native Norway at the end of 1826.
In December of 1828, he grew very sick. He did not recover and died on April 6. Two days later, not knowing that he had died, a messenger arrived letting his family know that Abel had secured a mathematical position in Berlin. Abel was 26.
Abel was the second person to attempt this proof. His predecessor Paolo Ruffini came very close. So close, in fact, that Augustin-Louis Cauchy believed that he had succeeded. In his honor, the proof is often called the Abel-Ruffini Theorem. In fairness to Abel, Ruffini made an assumption in his proof which turns out to be true but which Ruffini did not prove.
In today's blog, I will show the argument in Abel's original proof of 1824.
Lemma 1:
Let:
(p + p1S(1/2))(1/m) + (p - p1S(1/2))(-1/m)
be a function on 5 parameters y1, ..., y5
where p,p1,S are symmetric on the same 5 parameters and m ≥ 2.
Then:
this function returns m distinct values when its parameters are permuted
Proof:
(1) By Lemma 1, here, S(1/2) takes 2 distinct return values when its parameters are permuted and we can call these two values s1, s2 and we know that s1 = -s2
(2) So, it follows that the two cases gives us two possible expressions:
(p + p1s1)(1/m) + (p - p1s1)(1/m)
and
(p + p1s2)(1/m) + (p - p1s2)(-1/m)
(3) But, clearly:
(p + p1s1)(1/m) + (p - p1s1)(1/m) =(p + [-p1s2])(1/m) + (p - [-p1s2])(1/m) =
= (p - p1s2)(1/m) + (p + p1s2)(1/m)
(4) So, it follows that swapping s1 and s2 does not change the value, so the number of return values when the m parameters are permuted is m.
QED
Theorem 2: A solution to the general quintic equation is not expressible by radicals.
Proof:
(1) Assume that a solution to the general quintic equation can be expressed in radicals. That is we can state an equation for each root y in terms of a,b,c,d,e such that:
y5 - ay4 + by3 - cy2 + dy - e = 0
(2) If a solution to this equation exists, it can be represented as follows (see Theorem 5, here):

where m is a prime number and R, p2, ..., pm-1 are all functions of this same form finitely nested at the deepest level each p,pi,R is a function of the coefficients of the general quintic equation.
(3) Using this form [see Theorem 5, here], we further note that the distinct roots of the quintic equation are expressible in terms of R:
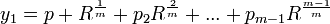

...
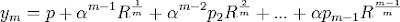
where α is an mth primitive root of unity [See here for a review of primitive roots of unity if needed]
(4) The Fundamental Theorem of Algebra gives us that the quintic equation has 5 roots. [See here for proof of the Fundamental Theorem of Algebra]
(5) Since this is the general solution, we can assume that each of the roots are distinct and that therefore, at the top level, m = 5.
(6) We can also state R(1/5) in terms of the roots (this was the gap that Ruffini assumed but did not prove). Using Corollary 5.1 here, we note that:
R(1/5) = (1/5)(y1 + α4y2 + ... + αy5)
(7) Now, by our result in step #2, we can assume that this same equation holds true at all levels. So at the lowest levels, we can assume that R is a rational function of the coefficients a,b,c,d,e.
(8) We can also show that at the bottom level, R is a function of the 5 roots. [See Corollary 3.1, here]
(9) Then, from step #7 and step #8, using Corollary 6.1, here, we can conclude that at the depeest level, m = 2.
(10) Now, we have two states to consider. Either the expression in step #2 consists of only two levels (at the top level m=5 and at the bottom level m=2) or its consists of more than two levels.
(11) So, if there exists a level above the lowest level but below the top level, then by step #2 above, it must be characterized by a prime m and by step #8 above we can assume that it is a function of the 5 roots.
(12) From Lagrange's Theorem (See Theorem, here), we can assume that if we permuted the 5 roots, the number of return values will divide 5! = 120.
(13) From Corollary 1.1, here and step #9 above, we know that the number of return values will be 2*m. Since 2*m must divide 120 and m must be a prime, we conclude that m=2, 3, or 5.
(14) But m ≠ 5, since from the reasoning of Corollary 1.1 in step #13, if m=5, then ultimately we would have 2*5*5*n return values which does not divide 120.
(15) We also know that m ≠ 2 since this gives us 2*2=4 return values and by Cauchy's Theorem (see Theorem 2, here), if the return values are less than 5, then it is 1 or 2.
(16) Further, we know that m ≠ 3 since:
(a) Let r = (p + p1S(1/2))(1/m)
where p,p1,S are symmetric with respect to the 5 roots of a quintic equation.
(b) Let r1 = (p - p1S(1/2))(1/m)
(c) So, we define a function on the 5 roots of the quintic equation such that:
f(y1, ..., y5) = r + r1
(d) From Lemma 1 above, such a function will return m distinct values when its m parameters are permuted.
(e) But, by Cauchy's Thereom used in step #15 above, if m is less than 5, it can only be 1 or 2.
(k) Hence, this means m ≠ 3.
(17) But, then it follows from steps #13, #14, #15, #16 above that the solution to the general quintic equation has only two levels and therefore the solution has the following form:

where m=5 and p,R,p2, ... p4 are functions of the form s + s1T(1/2) where s, T, s1 are rational functions of the coefficients of the quintic equation: a,b,c,d,e.
(18) Now, from step #6 above, we have:
R(1/5) = (1/5)(y1 + α4y2 + ... + αy5)
where α is a primitive 5th root of unity and y1, ..., y5 are the 5 distinct roots of a quintic equation.
(19) Now, from #17 above, we have:
R(1/5) = (s + s1T(1/2))(1/5)
where s, s1, T are symmetric on y1, ..., y5
(20) So, putting these two steps together gives us:
(1/5)(y1 + α4y2 + ... + αy5) = (s + s1T(1/2))(1/5)
(21) But this is clearly impossible since (1/5)(y1 + α4y2 + ... + αy5) can take 5!=120 distinct return values when its the parameters are permuted and (s + s1T(1/2))(1/5) can only take 2*5=10 distinct return values.
(22) Therefore, we have a contradiction and we reject our assumption in step #1.
QED
Corollary 2.1: A solution to the general n-th equation where n ≥ 6 is not expressible by radicals.
Proof
(1) Assume that a solution to a general n-th equation where n ≥ 6 is expressible by radicals.
(2) Let:
y5 - ay4 + by3 - cy2 + dy - e = 0
be a general quintic equation.
(3) Let i = n - 5 so that i ≥ 1.
(4) If we multiply (y - c1)*...*(y - ci)*(y5 - ay4 + by3 - cy2 + dy - e ), then we have an n-th equation.
(5) By assumption, we now solve this n-th equation so that our roots are y1, ..., y5, y6, ..., yn
(6) But then we have also solved the quintic equation using radicals which by Theorem 1 above is impossible.
(7) So, we have a contradiction and we reject our assumption in step #1.
QED
References
Abel printed a limited set copies of his proof in hopes of using it as a "calling card" when he visited the great mathematicians of his day. Because he was short on funds, Abel was forced to keep the proof as short and concise as possible. He had hoped to secure recognition and financial sponsorship from his trip. When he ran out of money, he returned to his native Norway at the end of 1826.
In December of 1828, he grew very sick. He did not recover and died on April 6. Two days later, not knowing that he had died, a messenger arrived letting his family know that Abel had secured a mathematical position in Berlin. Abel was 26.
Abel was the second person to attempt this proof. His predecessor Paolo Ruffini came very close. So close, in fact, that Augustin-Louis Cauchy believed that he had succeeded. In his honor, the proof is often called the Abel-Ruffini Theorem. In fairness to Abel, Ruffini made an assumption in his proof which turns out to be true but which Ruffini did not prove.
In today's blog, I will show the argument in Abel's original proof of 1824.
Lemma 1:
Let:
(p + p1S(1/2))(1/m) + (p - p1S(1/2))(-1/m)
be a function on 5 parameters y1, ..., y5
where p,p1,S are symmetric on the same 5 parameters and m ≥ 2.
Then:
this function returns m distinct values when its parameters are permuted
Proof:
(1) By Lemma 1, here, S(1/2) takes 2 distinct return values when its parameters are permuted and we can call these two values s1, s2 and we know that s1 = -s2
(2) So, it follows that the two cases gives us two possible expressions:
(p + p1s1)(1/m) + (p - p1s1)(1/m)
and
(p + p1s2)(1/m) + (p - p1s2)(-1/m)
(3) But, clearly:
(p + p1s1)(1/m) + (p - p1s1)(1/m) =(p + [-p1s2])(1/m) + (p - [-p1s2])(1/m) =
= (p - p1s2)(1/m) + (p + p1s2)(1/m)
(4) So, it follows that swapping s1 and s2 does not change the value, so the number of return values when the m parameters are permuted is m.
QED
Theorem 2: A solution to the general quintic equation is not expressible by radicals.
Proof:
(1) Assume that a solution to the general quintic equation can be expressed in radicals. That is we can state an equation for each root y in terms of a,b,c,d,e such that:
y5 - ay4 + by3 - cy2 + dy - e = 0
(2) If a solution to this equation exists, it can be represented as follows (see Theorem 5, here):

where m is a prime number and R, p2, ..., pm-1 are all functions of this same form finitely nested at the deepest level each p,pi,R is a function of the coefficients of the general quintic equation.
(3) Using this form [see Theorem 5, here], we further note that the distinct roots of the quintic equation are expressible in terms of R:
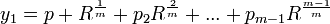

...
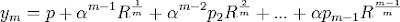
where α is an mth primitive root of unity [See here for a review of primitive roots of unity if needed]
(4) The Fundamental Theorem of Algebra gives us that the quintic equation has 5 roots. [See here for proof of the Fundamental Theorem of Algebra]
(5) Since this is the general solution, we can assume that each of the roots are distinct and that therefore, at the top level, m = 5.
(6) We can also state R(1/5) in terms of the roots (this was the gap that Ruffini assumed but did not prove). Using Corollary 5.1 here, we note that:
R(1/5) = (1/5)(y1 + α4y2 + ... + αy5)
(7) Now, by our result in step #2, we can assume that this same equation holds true at all levels. So at the lowest levels, we can assume that R is a rational function of the coefficients a,b,c,d,e.
(8) We can also show that at the bottom level, R is a function of the 5 roots. [See Corollary 3.1, here]
(9) Then, from step #7 and step #8, using Corollary 6.1, here, we can conclude that at the depeest level, m = 2.
(10) Now, we have two states to consider. Either the expression in step #2 consists of only two levels (at the top level m=5 and at the bottom level m=2) or its consists of more than two levels.
(11) So, if there exists a level above the lowest level but below the top level, then by step #2 above, it must be characterized by a prime m and by step #8 above we can assume that it is a function of the 5 roots.
(12) From Lagrange's Theorem (See Theorem, here), we can assume that if we permuted the 5 roots, the number of return values will divide 5! = 120.
(13) From Corollary 1.1, here and step #9 above, we know that the number of return values will be 2*m. Since 2*m must divide 120 and m must be a prime, we conclude that m=2, 3, or 5.
(14) But m ≠ 5, since from the reasoning of Corollary 1.1 in step #13, if m=5, then ultimately we would have 2*5*5*n return values which does not divide 120.
(15) We also know that m ≠ 2 since this gives us 2*2=4 return values and by Cauchy's Theorem (see Theorem 2, here), if the return values are less than 5, then it is 1 or 2.
(16) Further, we know that m ≠ 3 since:
(a) Let r = (p + p1S(1/2))(1/m)
where p,p1,S are symmetric with respect to the 5 roots of a quintic equation.
(b) Let r1 = (p - p1S(1/2))(1/m)
(c) So, we define a function on the 5 roots of the quintic equation such that:
f(y1, ..., y5) = r + r1
(d) From Lemma 1 above, such a function will return m distinct values when its m parameters are permuted.
(e) But, by Cauchy's Thereom used in step #15 above, if m is less than 5, it can only be 1 or 2.
(k) Hence, this means m ≠ 3.
(17) But, then it follows from steps #13, #14, #15, #16 above that the solution to the general quintic equation has only two levels and therefore the solution has the following form:

where m=5 and p,R,p2, ... p4 are functions of the form s + s1T(1/2) where s, T, s1 are rational functions of the coefficients of the quintic equation: a,b,c,d,e.
(18) Now, from step #6 above, we have:
R(1/5) = (1/5)(y1 + α4y2 + ... + αy5)
where α is a primitive 5th root of unity and y1, ..., y5 are the 5 distinct roots of a quintic equation.
(19) Now, from #17 above, we have:
R(1/5) = (s + s1T(1/2))(1/5)
where s, s1, T are symmetric on y1, ..., y5
(20) So, putting these two steps together gives us:
(1/5)(y1 + α4y2 + ... + αy5) = (s + s1T(1/2))(1/5)
(21) But this is clearly impossible since (1/5)(y1 + α4y2 + ... + αy5) can take 5!=120 distinct return values when its the parameters are permuted and (s + s1T(1/2))(1/5) can only take 2*5=10 distinct return values.
(22) Therefore, we have a contradiction and we reject our assumption in step #1.
QED
Corollary 2.1: A solution to the general n-th equation where n ≥ 6 is not expressible by radicals.
Proof
(1) Assume that a solution to a general n-th equation where n ≥ 6 is expressible by radicals.
(2) Let:
y5 - ay4 + by3 - cy2 + dy - e = 0
be a general quintic equation.
(3) Let i = n - 5 so that i ≥ 1.
(4) If we multiply (y - c1)*...*(y - ci)*(y5 - ay4 + by3 - cy2 + dy - e ), then we have an n-th equation.
(5) By assumption, we now solve this n-th equation so that our roots are y1, ..., y5, y6, ..., yn
(6) But then we have also solved the quintic equation using radicals which by Theorem 1 above is impossible.
(7) So, we have a contradiction and we reject our assumption in step #1.
QED
References
- Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004
- William Rowan Hamilton, "On the Argument of Abel", Transactions of the Royal Irish Academy, 18 (1839), pp 171-259.
Subscribe to:
Posts (Atom)
